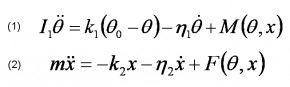Simulation

Synchronisation

Le concept de résonique a pu être simulé. Deux équations différentielles couplées par des forces magnétiques suffisent à démontrer numériquement la possibilité de synchroniser la vitesse de défilement d’un rouage et d’entretenir les oscillations d’un résonateur. Ces deux équations sont basées sur le principe de la deuxième loi de Newton qui lie l’accélération d’un corps de masse m avec la résultante des forces qu’il subit.

L’équation (1) modélise le mouvement angulaire du rouage. Le premier terme à gauche représente l’accélération angulaire du rotor et l’inertie totale du rouage, le deuxième terme le moment de force d’un barillet avec décroissance de force linéaire, le troisième terme le couple de force de frottement visqueux proportionnel à la vitesse de rotation, finalement le dernier terme le moment de force magnétique dépendant de la position de l’oscillateur et de l’angle du rotor.

L’équation (2) modélise le mouvement de l’oscillateur. Le premier terme à gauche représente l’accélération de l’oscillateur et sa masse équivalente, le deuxième terme la force de rappel élastique, le troisième terme les forces de frottement visqueuses proportionnelles à la vitesse, finalement le dernier terme la force magnétique dépendant de la position de l’oscillateur et de l’angle du rotor.

Les deux équations sont couplées par les forces magnétiques. Les forces magnétiques dépendent de la géométrie du rotor et de l’aimant ainsi que des matériaux utilisés. Elles sont calculées par la méthode des éléments finis pour chaque position angulaire du rotor et position de l’oscillateur.

L’analyse numérique par différences finies nous a permis de tester le concept. En modifiant les différents paramètres des équations, la simulation a permis de trouver des paliers de synchronisation. Une stabilisation de la vitesse du rouage et de l’amplitude de l’oscillateur est observée après une période transitoire. Sur la durée l’oscillateur compense la perte de moment de force du barillet ce qui permet de maintenir une synchronisation sur une échelle d’énergie assez large. Quelques perturbations aléatoires ont été ajoutées pour voir si la synchronisation tient. L’étude a permis de trouver des paliers avec des paramètres physiquement réalisables. Les simulations suffisent à confirmer les hypothèses et à dimensionner des prototypes qui fonctionnent.

Equations différentielles

I_1: moment d’inertie des rouages [kg ∙ m2] θ: angle parcouru par le rotor magnétique [rad] k_1: constante de couple du barillet [N ∙ m] θ_0: angle de parcours total du rotor [rad] η_1: coefficient de frottement [N ∙ m ∙ s] M(θ,x): moment de force magnétique [N ∙ m] m: masse équivalente [kg] x: déplacement de l’oscillateur [m] k_2: constante de raideur [N/m] η_2: coefficient d’amortissement [Ns/m] F(θ,x): force magnétique sur l’oscillateur [N]

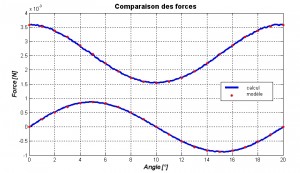
Force magnétique

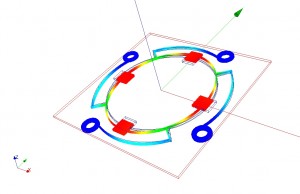
Les forces magnétiques ont été simulées par la méthode des éléments finis.  Cela permet de dimensionner la géométrie entre le rotor magnétique et les aimants permanents afin d’avoir un échange d’énergie par transmission d’une force la plus sinusoïdale possible lors d’une rotation à vitesse constante du rotor. Les simulations permettent de calculer les fonctions de couplage des deux équations différentielles précédentes.  Les simulations permettent de dimensionner une géométrie ou le champ magnétique permet un échange suffisant d’énergie mais reste très localisé afin de ne pas avoir d’effet perturbateur sur le reste des mécanismes.

Résonateur

Les résonateurs ont été simulés par la méthode des éléments finis, ainsi qu’avec différents modèles analytiques de prise en compte des pertes, flux de chaleur, frottement aérien, absorption par le support, et vibrations parasites. Les simulations permettent de tester les différents modes de vibrations. Cela permet d’atteindre les fréquences et puissances voulues. Elles permettent de tester les formes et matériaux qui donnent les meilleurs facteurs de qualité possible.