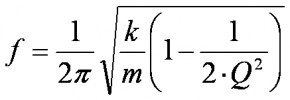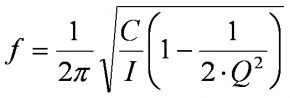As the regulating organ, the oscillator divides time. It is the watch’s most important mechanism because accuracy is directly depending on its precision and stability. The higher the resonator’s frequency is, the higher the watch’s accuracy will be. This is especially true for a wristwatch. High-frequency regulating organs are more accurate because:
– Improving a watch’s chronometric performance is directly related to increasing the time base Q factor and the latter is largerly determined by its natural frequency. Increasing the frequency allows a higher Q factor.
– Statistically, in relation to disturbance induced timing variations proportional to the duration of the oscillation, the shorter the oscillation’s period is, i.e the higher frequency, the smaller the timing variations will be.
– A resonator’s balancing default will induce perturbations in wearing condition inversely proportional to the square of the frequency. Therefore, the faster the frequency is, the smaller the impact of unbalanced resonator.
The sonic oscillator replaces the usual balance-spring oscillator in mechanical watches. The balance-spring is a resonator in which the inertia part (balance wheel) is separated from the oscillator (hairspring). The standard hairspring is very flexible, not free-standing and therefore, necessitates guiding through the pivots, which induces friction. Résonique proposes a different approach where inertia and spring are merged into one single part. Rigid and free-standing, the resonator is used with its natural frequency and normal modes shape determined by the attachment points, geometry and the material’s specifications. Accuracy does not require a wide amplitude with these oscillators. Today’s resonators developed by De Bethune cover a wide frequency range from 20 Hz to 20 kHz.
 |
 |
 |
|
Various resonators and rotors |
||
The characteristics of mechanical resonators are related to their geometry, the material’s elastic deformation property, and mass or inertia. As per equation (1), frequency depends on the global stiffness and equivalent mass. A high Q factor ensures a very stable frequency. The oscillator’s power also depends on those properties as well as oscillations’ amplitude, as per equation (2). The resonator’s regulating power is proportional to the oscillator’s power. The greater the power, the lower will be the impact of disturbances on the oscillator.
|
 |
|||||||||
|
High frequency strategy
From equation (2), we can determine that higher frequency has a very strong effect on the oscillator’s power. In order to remain in an acceptable energy range, De Bethune’s strategy is to considerably reduce the oscillator’s amplitude. This is the reason why De Bethune is developing low amplitude oscillators. Both the Q factor and isochronism are better at low amplitude. If the oscillator’s Q factor could be improved, proportionally so could the power, and therefore the power required to sustain the oscillator remains equivalent as per equation (3). For a given power consumption level, such a regulating organ will run at a higher frequency, higher Q factor, and higher regulating power. These combined improvements will greatly improve chronometric performance.
Example
Let’s consider a specific case comparing a classical 4 Hz balance-spring escapement with a Résonique 800 Hz escapement. Frequency is multiplied by 200. From equation (2) we can determine that power will be multiplied by 8’000’000 times if amplitude remains the same. If we reduce amplitude by dividing it by 894, the oscillator’s power is now 10 times greater than the balance-spring model. If we consider that the Q factor is also multiplied by 10, we end up with the same power consumption for regulating power 10 times greater, as per equation (4).
There is still a wide field of research on the resonator to find the ideal geometry and the best compromise between power and Q factor according to the frequency.